백준 2166

문제

2차원 평면상에 N(3 ≤ N ≤ 10,000)개의 점으로 이루어진 다각형이 있다. 이 다각형의 면적을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 N이 주어진다. 다음 N개의 줄에는 다각형을 이루는 순서대로 N개의 점의 x, y좌표가 주어진다. 좌표값은 절댓값이 100,000을 넘지 않는 정수이다.

출력

첫째 줄에 면적을 출력한다. 면적을 출력할 때에는 소수점 아래 둘째 자리에서 반올림하여 첫째 자리까지 출력한다.

예제 입력 1

4
0 0
0 10
10 10
10 0

예제 출력 1

100.0

풀이(kotlin)

 - 2차원 평면에서 좌표를 알때 면적을 구하는 공식을 사용하였다.

 

 - 예를들어 2차원 평면에서 세 점의 좌표를 (x1,y1), (x2,y2), (x3,y3)라 할 때, 세 점을 꼭지점으로 하는 삼각형의 넓이를 일반적으로 구해 보자.

 

1. 헤론의 공식

 

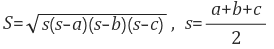
 - 삼각형의 세 변의 길이를 a, b, c라 할 때 위 식을 이용하면 손쉽게 삼각형 면적을 계산할 수 있습니다.

 

2. 벡터의 외적

 - 벡터의 외적은 3차원 벡터에서 정의되기 때문에 z = 0으로 생각하고 문제를 적용합니다. 즉, 3차원 공간에서 세 점 (x1,y1,0), (x2,y2,0), (x3,y3,0)이 이루는 삼각형 면적을 구하는 문제로 생각합니다. 두 변을 이루는 벡터를

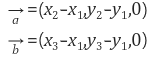
 - 로 잡으면 삼각형의 면적은 |a × b|/2 와 같습니다 (두 벡터의 외적의 크기는 두 벡터를 두 변으로 하는 평행사변형의 넓이).

 - a × b = (0, 0, (x2-x1)(y3-y1)-(x3-x1)(y2-y1))이므로 구하는 삼각형의 면적은 다음과 같습니다.

 

 

[적용 방법]

 - 위 공식 중 벡터의 외적을 이용하여 다각형을 여러개의 삼격형으로 나누어서 값을 더해주는 방식으로 문제를 풀이하였다.

 

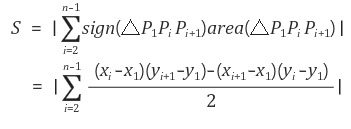
import kotlin.math.abs

private val r = System.`in`.bufferedReader()

fun main() {
    val N = r.readLine().toInt()
    val x = LongArray(N)
    val y = LongArray(N)
    repeat(N) { i ->
        r.readLine().split(" ").map { it.toLong() }.apply {
            x[i] = this[0]
            y[i] = this[1]
        }
    }

    var area = 0.0
    for (i in 1 until N-1) {
        area += ((x[i] - x[0]) * (y[i+1] - y[0])).toDouble()/2 - ((x[i+1] - x[0]) * (y[i] - y[0])).toDouble()/2
    }
    println(String.format("%.1f", abs(area)))
}